Математический маятник

Математический маятник. Чёрный пунктир — положение равновесия, [math]\displaystyle{ \theta }[/math] — угол отклонения от вертикали в некоторый момент

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен

[math]\displaystyle{ T_0 = 2\pi \sqrt{L \over g} }[/math]

и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.

Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.

Характер движения маятника

Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, следовательно, является системой с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, получится система с двумя степенями свободы (так как становятся возможными колебания по двум горизонтальным координатам).

При колебаниях в одной плоскости маятник движется по дуге окружности радиуса [math]\displaystyle{ L }[/math], а при наличии двух степеней свободы может описывать кривые на сфере того же радиуса. Нередко, в том числе в случае нити, ограничиваются анализом плоского движения; оно и рассматривается далее.

Уравнение колебаний маятника

Маятник (схема с обозначениями)

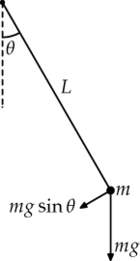
Если в записи второго закона Ньютона [math]\displaystyle{ m\vec{a} = \vec{F} }[/math] для математического маятника выделить тангенциальную составляющую ([math]\displaystyle{ ma_{\tau} = F_{\tau}) }[/math], получится выражение

[math]\displaystyle{ mL\ddot \theta = -mg\sin\theta }[/math],

так как [math]\displaystyle{ a_{\tau} = \dot v = d/dt(Ld\theta/dt) }[/math], а из действующих на точку сил тяжести и натяжения ненулевую компоненту [math]\displaystyle{ F_{\tau} }[/math] даёт только первая. Следовательно, колебания маятника описываются обыкновенным дифференциальным уравнением (ДУ) вида

[math]\displaystyle{ \ddot \theta + \frac{g}{L} \sin\theta = 0 }[/math],

где неизвестная функция [math]\displaystyle{ \theta(t) }[/math] ― это угол отклонения маятника в момент [math]\displaystyle{ t }[/math] от нижнего положения равновесия, выраженный в радианах, [math]\displaystyle{ L }[/math] ― длина подвеса, [math]\displaystyle{ g }[/math] ― ускорение свободного падения. Предполагается, что потерь энергии в системе нет. В области малых углов [math]\displaystyle{ \sin\theta\approx\theta }[/math] это уравнение превращается в

[math]\displaystyle{ \ddot \theta + \frac{g}{L} \theta = 0 }[/math].

Для решения ДУ второго порядка, то есть для определения закона движения маятника, необходимо задать два начальных условия — угол [math]\displaystyle{ \theta }[/math] и его производную [math]\displaystyle{ \dot\theta }[/math] при [math]\displaystyle{ t=0 }[/math].

Решения уравнения движения

Возможные типы решений

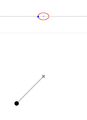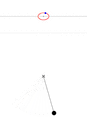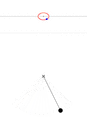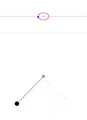
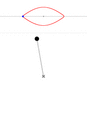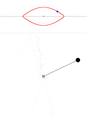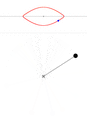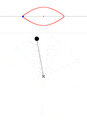
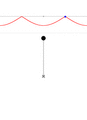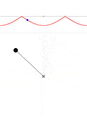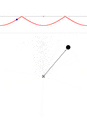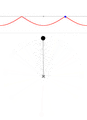
В общем случае решение ДУ с начальными условиями для маятника может быть получено численно. Варианты движения (в случае, если маятник — это материальная точка на лёгком стержне), качественно, представлены на анимации. В каждом окне вверху показана зависимость угловой скорости [math]\displaystyle{ \dot\theta }[/math] от угла [math]\displaystyle{ \theta }[/math]. По мере нарастания размаха поведение маятника всё сильнее отклоняется от режима гармонических колебаний.

• 

  Маятник висит

• 

  Малые колебания (размах 45°)

• 

  Колебания с размахом 90°

• 

  Колебания с размахом 135°

• 

  Колебания с размахом 170°

• 

  Фиксация в верхнем положении

• 

  Движение близкое к сепаратрисе

• 

  Вращение маятника

Гармонические колебания

Уравнение малых колебаний маятника около нижнего положения равновесия, когда уместна замена [math]\displaystyle{ \sin\theta\approx\theta }[/math], называется гармоническим уравнением:

[math]\displaystyle{ \ddot \theta + \omega_0^2 \theta = 0 }[/math],

где [math]\displaystyle{ \omega_0 = \sqrt{g/L} }[/math] ― положительная константа, определяемая только из параметров маятника и имеющая смысл собственной частоты колебаний. Кроме того, может быть осуществлён переход к переменной «горизонтальная координата» [math]\displaystyle{ x = L\sin\theta\approx L\theta }[/math] (ось [math]\displaystyle{ x }[/math] лежит в плоскости качания и ортогональна нити в нижней точке):

[math]\displaystyle{ \ddot x + \omega_0^2 x = 0 }[/math].

Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону:

[math]\displaystyle{ x = A \sin(\omega_0 t + \alpha) }[/math],

где [math]\displaystyle{ A }[/math] — амплитуда колебаний маятника, [math]\displaystyle{ \alpha }[/math] — начальная фаза колебаний.

Если пользоваться переменной [math]\displaystyle{ x }[/math], то при [math]\displaystyle{ t=0 }[/math] необходимо задать координату [math]\displaystyle{ x_0 }[/math] и скорость [math]\displaystyle{ v_{x0} }[/math], что позволит найти две независимые константы [math]\displaystyle{ A }[/math], [math]\displaystyle{ \alpha }[/math] из соотношений [math]\displaystyle{ x_0 = A\sin\alpha }[/math] и [math]\displaystyle{ v_{x0} = A\omega_0\cos\alpha }[/math].

Случай нелинейных колебаний

Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:

[math]\displaystyle{ \sin \frac{\theta}{2} = \varkappa \cdot \operatorname{sn}(\omega_0 t; \varkappa), }[/math]

где [math]\displaystyle{ \operatorname {sn} }[/math] — это синус Якоби. Для [math]\displaystyle{ \varkappa \lt 1 }[/math] он является периодической функцией, при малых [math]\displaystyle{ \varkappa }[/math] совпадает с обычным тригонометрическим синусом.

Параметр [math]\displaystyle{ \varkappa }[/math] определяется выражением

[math]\displaystyle{ \varkappa = \frac{\varepsilon+\omega_0^2}{2\omega_0^2},\quad \varepsilon = \frac{E}{mL^2} }[/math].

Период колебаний нелинейного маятника составляет

[math]\displaystyle{ T = \frac{2\pi}{\Omega}, \quad \Omega = \frac{\pi}{2}\frac{\omega_0}{K(\varkappa)} }[/math],

где K — эллиптический интеграл первого рода.

Для вычислений практически удобно разлагать эллиптический интеграл в ряд:

[math]\displaystyle{ T = T_0 \left\{1 + \left(\frac{1}{2}\right)^2 \sin^{2}\left(\frac{\theta_0}{2}\right) + \left(\frac{1 \cdot 3}{2 \cdot 4}\right)^2 \sin^{4}\left(\frac{\theta_0}{2}\right) + \dots + \left[\frac{\left(2n - 1\right)!!}{\left(2n\right)!!}\right]^2 \sin^{2n}\left(\frac{\theta_0}{2}\right) + \dots \right\} }[/math]

где [math]\displaystyle{ T_0 = 2\pi \sqrt\frac{L}{g} }[/math] — период малых колебаний, [math]\displaystyle{ \theta_0 }[/math] — максимальный угол отклонения маятника от вертикали.

При углах до 1 радиана (≈ 60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:

[math]\displaystyle{ T = T_0 \left( 1 + \frac{1}{4}\sin^{2}\left(\frac{\theta_0}{2}\right) \right) }[/math].

Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года:

[math]\displaystyle{ T = \frac{2\pi}{M\big(\cos(\theta_0/2)\big)} \sqrt\frac{L}{g} }[/math],

где [math]\displaystyle{ M(s) }[/math] — арифметико-геометрическое среднее чисел 1 и [math]\displaystyle{ s }[/math].

Движение по сепаратрисе

Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.

Факты

Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.

• Если амплитуда колебания маятника близка к [math]\displaystyle{ \pi }[/math], то есть движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения.
• Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
• В условиях вращения Земли при достаточно длинной нити подвеса плоскость, в которой маятник совершает колебания, будет медленно поворачиваться относительно земной поверхности в сторону, противоположную направлению вращения Земли (маятник Фуко).

Ссылки

• Коллекция Java-апплетов, моделирующая поведение математических маятников, в частности маятника Капицы.
• Java-апплет, моделирующий колебание математического маятника при наличии вязкого трения с черчением фазовой траектории.
• Учебный фильм "Математический и физический маятник", производство СССР

См. также

• Физический маятник
• Маятник Фуко